聚类算法实战:唐朝诗人们的聚类
2017-04-16
项目源代码参见 GitHub Repo
前一段时间在微信里看到了一篇分析唐朝诗人引用关系的文章,觉得还比较有意思。正好最近看了一些讲聚类算法的书,就突发奇想想看看算法是怎么理解那些伟大的诗人们的。比如通过诗人们在诗中的用词习惯来分析他们之间可能产生的聚类关系。
数据准备
要分析唐朝诗人,最好的数据来源当然是全唐诗了。这里我也直接使用了MrQianJinSi Github里的数据。
分词工具
因为我希望得到的数据是一张 { 诗人:{ 诗中词汇:词频 } } 的嵌套字典表,那么对全唐诗进行分词就是必要的步骤。这里我也直接使用了清华大学NLP实验室的thulac分词工具。需要注意的是,目前的thulac版本中的词性标注模型似乎只能支持PYTHON3.0之后的版本。所以,早点升级才是王道啊。
数据整理
通过分词工具,我们可以整理出来全唐诗中出现的不重复的字词有大概35w之多,诗人们大概有2600多位。
对于这么庞大的数据集直接聚类肯定没有什么意义。所以我首先需要对诗人们进行一个筛选,这里也沿用了[MrQianJinSi] (https://github.com/MrQianJinSi/poetry_analyzer)在文章里使用的初盛中晚这唐朝的四个时期当中比较有名气的一共150多位诗人作为分析的标准,将其他诗人从数据集中拿出。重新计算词频。字词数减少了大概9w多,但是还有将近25w左右不重复的字词。
那么我做的第二步就是减少要分析的词汇数量。我们知道,汉语当中有大量其实并没有什么实际意义,但是为了句子通顺仍然会被大量使用的字词。与此同时,还有些诗人会在诗中使用一些很生僻的字词,那么显然对这两种词汇的分析并没有什么意义。因此我们希望能把这两种词汇去掉。
所以,我对数据集中诗人们使用词汇的频率做了一个统计。
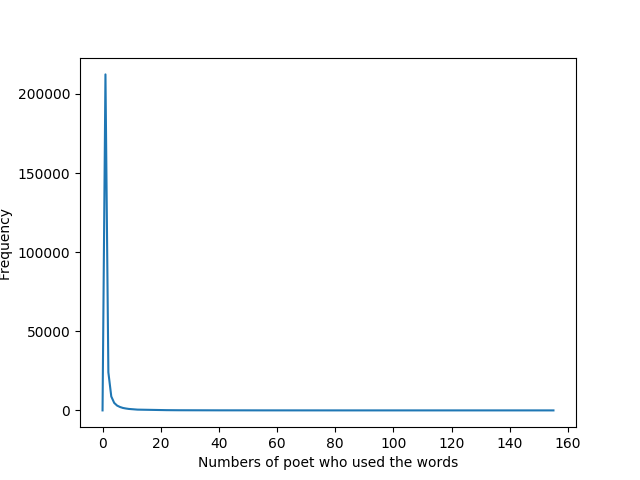
这里的横轴表示词被多少诗人使用过,竖轴表示有多少个词被x个诗人使用过。显而易见,有十分巨量的词汇只被个位数的诗人使用过,所以我设定了我的第一个参数,minFraction = 0.1,也即是说,我希望我所分析的词汇最起码被十分之一的诗人,也就是15位诗人使用过。
现在,设定所有被15位以下的诗人使用过的词汇数量为0:
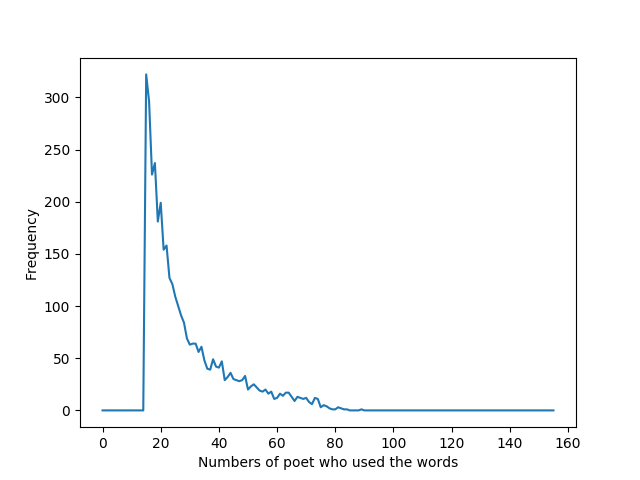
我们可以看到被60位以上诗人同时使用的词汇渐渐收敛,所以设定我的第二个参数maxFraction=0.4,也即是说,我希望我所分析的词汇最多被五分之二的诗人使用,否则,大量常用词汇的出现就会使我们的分析没有了意义。
度量方法
因为全唐诗中收录每位诗人的诗词数量是不统一的,所以我在这里选择了皮尔逊相关性来尝试拟合诗人们之间的关系。
关于度量方法更多的解释可以参见我之前实践推荐算法的文章。
k值的选择
在尝试实施算法之前,我设想的比较有意义的k值应该是4,因为其实诗人们的数据集是非常明显的以初盛中晚这四个时代来划分的。但是,当我实现了算法并实际聚类之后,发现这样的聚类没有什么意义,四个时代的诗人非常没有规律的分步在了四个簇中,很难提取什么有效的信息。
因此我这里选择了一个比较随意的k=15,即希望算法可以将诗人聚类成十类以此来希望提取一些比较有意思的信息。必须承认,这样的随缘选择法是非常不严谨的。我也尝试去给定一个类簇指标然后去计算指标关于K值的变化图像(如下图)。但是并没有得到一个很好的“肘部”转折点。
指标:所有类簇的平均质心距离的加权平均值
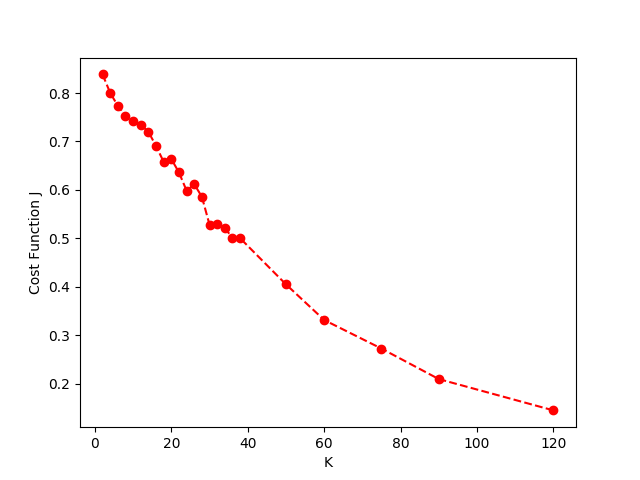
核心算法
在聚类前,我将我的数据集整理成为了一个嵌套list(也可以理解为矩阵),其中的每一列代表的一个词汇,每一行代表的是一位诗人,那么a_i_j就对应的是诗人i使用词汇j的次数。
因此,算法步骤如下:
-
遍历数据集,计算每一列的取值区间
-
重复k次:遍历数据,在每一列的取值区间中随机生成类簇中心标量,从而得到一个类簇中心向量
- 遍历数据集:
- 对每一行数据向量,计算与其最匹配的类簇,将其分配到该类簇
-
存储分配结果,并比较本次迭代与前一次迭代分配结果
-
如果相同,那么意味着我们的聚类收敛,结束迭代
- 否则,遍历类簇,重新计算类簇中心向量
def doKcluster(self, k=4, distance = pearson):
rows = self.processedPoetWordsList
#Calculate range for each word
ranges = [(min([row[i] for row in rows]), max([row[i] for row in rows]))
for i in range(len(rows[0]))]
#Random creat k clusters
clusters = [[random.random() * (ranges[i][1] - ranges[i][0]) + ranges[i][0]
for i in range(len(rows[0]))]
for j in range(k)]
lastMatches = None
for t in range(150):
print("Iteration %d" %t)
bestMatches = [[] for i in range(k)]
#Find the closet cluster for each line
for iRow in range(len(rows)):
row = rows[iRow]
bestMatch, bestDistance = 0, 1
for i in range(k):
d = distance(clusters[i], row)
if d < bestDistance :
bestDistance = d
bestMatch = i
bestMatches[bestMatch].append(iRow)
#If convergence
if bestMatches == lastMatches:
print("Converge break")
break
lastMatches = bestMatches
#Move clusters
for i in range(k):
if len(bestMatches[i])>0:
cList = []
for idxRow in bestMatches[i]:
cList.append(rows[idxRow])
clusters[i] = np.average(cList, axis=0).tolist()
J = self.computeCostFunction(clusters, bestMatches, distance)
return bestMatches, J, clusters
聚类结果
其实聚类的结果并没有像我当初想象的那样理所当然,比如并不是所有的边塞诗人自然的成为了一个类簇,这其中当然有很多解释,比如不是所有的边塞诗人这辈子都只写了边塞诗。或者,从汉语上来说,一个人诗词文章的风格不一定跟他的用词是强相关的,更多的可能是词语组合之后的意向与气度。
但还是出现了一些比较有意思的组合,比如:
******** Cluster No.11 ********
元稹:3
柳宗元:3
聂夷中:4
白居易:3
陆龟蒙:4
卢纶:3
杜牧:4
皮日休:4
方干:4
杜荀鹤:4
黄滔:4
******** End ********
中唐和晚唐最著名的两对好基友“元白”和“皮陆”居然出现在了同一簇中。更何况还有小李杜中的杜牧和独钓寒江雪的柳宗元。从知名度上来说,这一簇在所有类簇中独占鳌头。
注:诗人后面的数字代表的是他们的朝代,从0-3分别对应着初盛中晚四个时期。
还有
******** Cluster No.10 ********
韦应物:3
杜甫:2
王之涣:2
戴叔伦:3
顾况:3
令狐楚:4
施肩吾:3
张乔:4
韩偓:4
******** End ********
在这一类簇中,令狐楚,杜甫这三绝当中的两人赫然在列,至于为何独独缺了韩愈。大概是因为韩愈是以古文而非诗词著称吧。
Remark
因为K均值聚类其实本质上还是一个局部最优解的聚类,因此在跑算法的过程中,对同一个k值,我并没有能够得到一个比较稳定的结果。所以,下面有时间的话也想在本次数据集的基础上实现层级聚类算法,也许会更有实际意义。