支持向量机的序列最小最优化算法SMO实现

2017-04-09

本篇文章涉及代码和测试集可以参见GitHub Repo

最近在看李航教授的《统计学习方法》的过程中，发现支持向量机部分的SMO算法的数理部分第一次看的时候有点吃力，反复看了两三遍才算勉强弄明白了证明和推导过程。作为一个所谓的工程师，遇到比较晦涩的理论脑袋里面浮现的第一个念头当然就是去实践它。上网查了一下，果然有JustForCS和刘洪江两位同道已经完成了SMO算法实现的代码。

但是仔细研究了一下代码，发现他们的代码中都对违反KKT原则条件做了更近一步的推导和对SMO选择变量部分做了一些简化。原书中对于选择变量的算法是以最违反KKT原则的alpha_i作为锚定的第一变量，下降最大的alpha_j作为选定的第二变量继而更新alpha值。而在这两位的代码中，他们都选择了随机选择变量然后计算优化步长来决定是否使用变量。

所以在这里也打算以《统计学习方法》一书中的算法作为标准，手动实现SMO算法。当然这样并不意味着就一定比上面两位的实现方式要好，只不过是更贴近书中算法的说明从而更容易理解。

对于支持向量机比较全面的描述可以参考文章。

这里直接给出《统计学习方法》一书中关于SMO的算法说明。

SMO算法

输入：

训练数据集 $ T= \{ ({x_1},{y_1}),({x_2},{y_2}), \cdot \cdot \cdot ,({x_N},{y_N}) \} $

其中$ {x_i} \in \chi \in {\mathbb{R}^n}$，${y_i} \in \{-1,+1\}$，$i=1,2,\cdot\cdot\cdot,N$，精度$\varepsilon$。

输出：近似解$\hat a$

算法描述：

(1) 取初始值${a^{(0)}}=0$，令$K=0$

(2) 选取优化变量 ${a_1^{(k)}}$ , ${a_2^{(k)}}$ , 针对优化问题，求得最优解 ${a_1^{(k+1)}}$ , ${a_2^{(k+1)}}$ 并且更新 ${a^{(k)}}$ 为 ${a^{(k+1)}}$ 。

(3) 在精度条件范围内是否满足停机条件，即是否有变量违反KKT条件，如果违反了，则令$k=k+1$，跳转(2)，否则(4)。

(4) 求得近似解$\hat a = a^{(k+1)}$

下面就对(2)，(3)步分别解释。

违反KKT条件

违反KKT条件在我们的算法步骤(3)中，首先是用来作为停机条件，即当所有变量满足KKT条件时候，迭代计算停止。

SMO的核心解法是通过svm的原始问题，构造拉格朗日函数，并求解对偶换算得出的最优化问题。而通过定理，我们可以知道对偶问题等价的是对偶问题的KKT条件，换句话说，就是只要找到对应的${a^*}$满足了下列KKT条件，那么原始问题和对偶问题就解决了。

SVM的对偶问题对应的KKT条件为：

$$\begin{array}{l} \quad {a_i} = 0 \quad \Leftrightarrow \quad {y_i}g({x_i}) \ge 1\\ 0 < {a_i} < C \quad \Leftrightarrow \quad {y_i}g({x_i}) = 1\\ \quad {a_i} = C \quad \Leftrightarrow \quad {y_i}g({x_i}) \le 1 \end{array}$$

其中:

$$g(x) = \sum\limits_{i = 1}^N { {a_i}{y_i}K({x_i},{x_j}) + b}$$

因为计算机在计算的时候是有精度范围的，所以我们引入一个计算精度值$\varepsilon$，那么KKT条件就变成了：

$$\begin{array}{l} {a_i} = 0 \Leftrightarrow {y_i}g({x_i}) \ge 1 - \varepsilon \\ 0 < {a_i} < C \Leftrightarrow 1 - \varepsilon \le {y_i}g({x_i}) \le 1 + \varepsilon \\ {a_i} = C \Leftrightarrow {y_i}g({x_i}) \le 1 + \varepsilon \end{array}$$

那么相应的违规KKT条件的分量应该满足下列不等式：

$${\rm{Against\ KKT:}}$$ $$\begin{array}{l} {a_i} = 0 \Leftrightarrow {y_i}g({x_i}) > 1 - \varepsilon \\ 0 < {a_i} < C \Leftrightarrow 1 - \varepsilon > {y_i}g({x_i}) or {y_i}g({x_i}) > 1 + \varepsilon \\ {a_i} = C \Leftrightarrow {y_i}g({x_i}) > 1 + \varepsilon \end{array}$$

其实，通过推导，我们可以得到一个更简单的形式：

$${\rm{Against\ KKT:}}$$ $$\begin{array}{l} {a_i} < C \quad \Leftrightarrow \quad - \varepsilon > {y_i}{E_i}\\ 0 < {a_i} \quad \Leftrightarrow \quad {y_i}{E_i} > + \varepsilon \end{array}$$

其中：

${E_i} = g({x_i}) - {y_i}$ 因为$g({x})$其实就是决策函数，所以${E_i}$可以认为是对输入的${x_i}$的预测值与真实输出${y_i}$之差。

但是就像我之前说的，为了便于理解书中算法，这里我还是坚持使用的KKT条件的原始形式。

变量选取

KKT条件在我们的算法步骤(2)中，是选取变量的重要参考标准。 变量选取分为两步，第一步是选取违反KKT条件最严重的${a_i}$，第二步是根据已经选取的第一个变量，选择优化程度最大的第二个变量。

第一个变量的选取

SMO算法把选择第一个变量的过程称为外层循环，外层循环在训练样本中选取违反KKT条件最严重的样本点，并将其对应的变量作为第一个变量。

在这里，我对违反最严重的样本点的理解是与其对应的KKT条件绝对值差最大。

因此构建如下代码：

• 遍历样本点
• 针对${a_i}$取值区间，计算违反KKT绝对值差
• 取${a_i}$使违反KKT绝对值差最大

第二个变量的选取

SMO算法把选择第二个变量的过程称为内层循环。第二个变量j选择的标准是希望能使${a_2}$有足够大的变化。由书中公式可知，新值${a_2^{new}}$是依赖于$\left| {E_1 - E_2} \right|$的，并且此时${a_1}$已知因此$E_1$已知。

所以构建代码如下：

• 如果已选择${a_1}$则继续执行以下步骤，否则跳过（所有alpha都满足KKT条件，即达到停机条件）
• 遍历在第一变量选择计算中构建好的E值集
• 如果$E_1$为正，则选取${a_2}$使$E_2$最小
• 如果$E_1$为负，则选取${a_2}$使$E_2$最大

计算选取变量的新值

当我们完成了对第一第二变量的选择之后，就可以计算针对这两个变量的新值。首先计算出来的新值必须满足约束条件$\sum\limits_{i = 1}^N { {a_i}{y_i} = 0}$ ，那么求出来的${a_2^{new}}$需要满足下列条件（具体推导见《统计学习方法》的7.4.1）:

$$\begin{array}{l} L \le a_2^{new} \le H\\ L = \max (0,a_2^{old} - a_1^{old}),H = \min (C,C + a_2^{old} - a_1^{old}), \qquad {y_1} \ne {y_2}\\ L = \max (0,a_2^{old} + a_1^{old} - C),H = \min (C,a_2^{old} + a_1^{old}), \qquad {y_1} = {y_2} \end{array}$$

未经过裁剪的${a_2}$的解为：

$$\begin{array}{l} {a_2^{new,unc}} = {a_2^{old}} + \frac{ {y_2}({E_1}-{E_2)}}{\eta} \\ \eta = K_{11} + K_{22} - 2{K_{12}} \end{array}$$

裁剪后的解为

$$a_2^{new} = \left\{ \begin{array}{l} H,a_2^{new,unc} > H\\ a_2^{new,unc},L \le a_2^{new,unc} \le H\\ L,a_2^{new,unc} < L \end{array} \right.$$

第一个变量的解为

$$a_1^{new} = a_1^{old} + {y_1}{y_2}(a_2^{old} - a_2^{new})$$

还需要更新$b$:

$$\begin{array}{l} b_1^{new} = - {E_1} - {y_1}{K_{11}}(a_1^{new} - a_1^{old}) - {y_2}{K_{21}}(a_2^{new} - a_2^{old}) + {b^{old}}\\ b_2^{new} = - {E_2} - {y_1}{K_{12}}(a_1^{new} - a_1^{old}) - {y_2}{K_{22}}(a_2^{new} - a_2^{old}) + {b^{old}} \end{array}$$

在更新$b$时，如果有$0 \lt a_1^{new} \lt C$, 则$b^{new}=b_1^{new}$，如果有$0 \lt a_2^{new} \lt C$, 则 $b^{new}=b_2^{new}$， 否则$b^{new}=\frac{b_1^{new} + b_2^{new}}{2}$。

Remarks

在实施代码的过程中，我维护了两张屏蔽字典用来实现重新选择变量的机制：

• 在计算${a_2^{new}}$的最终解也就是裁剪解的时候，如果有L=H，那么我们将当前第二变量j加入屏蔽字典，重新选择一个新的第二变量j。
• 在计算出${a_2^{new}}$之后，我计算了一下本次迭代的步长，如果小于一个阈值，则我们认为本次迭代没有起到很好的优化效果，因此将当前第二变量j加入屏蔽字典，重新选择一个新的第二变量j。
• 如果对于选择的第一变量i，所有第二变量都被屏蔽，那么我们将当前第一变量i将入屏蔽字典。重新选择第一变量i。
• 每一次迭代结束后，清空两张屏蔽字典，准备下次迭代。

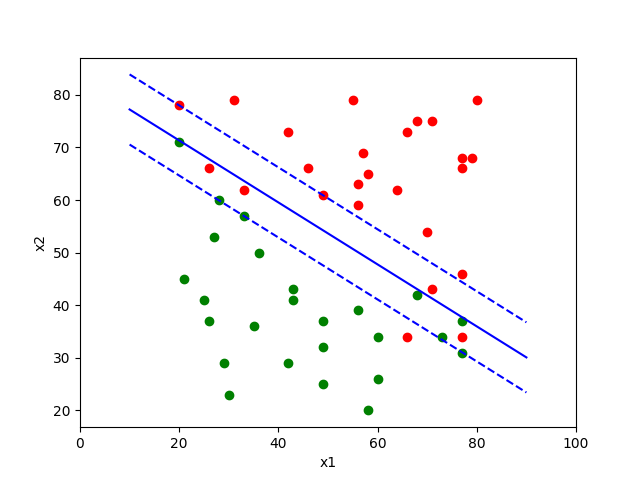
实例

以上算法的最终实施代码可以参见GitHub Repo

当C为0.05，$\varepsilon$为0.01，最大迭代为500时候，我们可以得到一个效果不错的分类器：